Efter videon följer ett problem som du kan lösa för att testa att du tillgodogjort dig innehållet.
Problem:
Beräkna den itererade integralen\[\int_0^{\pi} \left(\int_y^{\pi} \dfrac{\sin x}{x} \, dx\right)dy.\]Svar:
Vi skriver om integralen som en dubbelintegral:\[\int_0^{\pi} \left(\int_y^{\pi} \dfrac{\sin x}{x} \, dx\right)dy=\iint_{\Omega} \dfrac{\sin x}{x} \, dxdy,\]där\[\Omega =\{(x,y): y\le x\le {\pi}, 0\le y\le {\pi}\}=\]\[\{(x,y): 0\le y\le x, 0\le x\le {\pi}\}.\]Dubbelintegralen kan nu beräknas som\[\iint_{\Omega} \dfrac{\sin x}{x} \, dxdy=\int_0^{\pi} \left(\int_0^x \dfrac{\sin x}{x} \, dy\right)dx=\]\[\int_0^{\pi} \dfrac{\sin x}{x}\cdot x \,dx=\int_0^{\pi} \sin x\, dx=\]\[\Big[-\cos x\Big]_0^{\pi}=1-(-1)=2.\]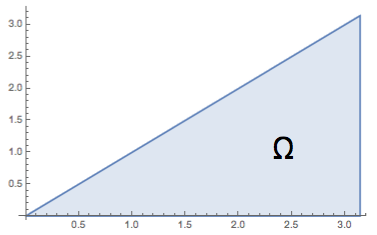

Maila för handledning.
Hur upplevde du problemet?
Svårighet:
Relevans:
Svårighet:
Relevans: