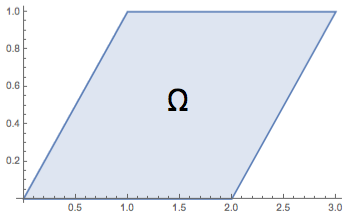
Normalt sett är det bäst att integrera med avseende på $x$ innerst. Det beror på att området kan beskrivas som\[\Omega =\{ (x,y): y\le x\le y+2, 0\le y\le 1\}.\]Om vi i stället försöker skriva området på formen\[\Omega =\{ (x,y): \varphi(x)\le y\le\psi(x), a\le x\le b\},\]så kan inte $\varphi$ och $\psi$ uttryckas på ett lika enkelt sätt. $\varphi$ blir den funktion som är lika med $0$ på $[0,2]$, och lika med $x-2$ på $[1,3]$. På motsvarande sätt blir $\psi$ den funktion som är lika med $x$ på $[0,1]$, och lika med $1$ på $[1,3]$. För att beräkna den inre integralen måste vi normalt behandla intervallen $[0,1]$, $[1,2]$ och $[2,3]$ separat.
(Naturligtvis går det att hitta exempel där integranden är av en sådan typ att det ändå är bättre att integrera innerst med avseende på $y$.)