Efter videon följer ett problem som du kan lösa för att testa att du tillgodogjort dig innehållet.
Problem:
Ett analytiskt sätt att beskriva ett Möbius-band är genom avbildningen \(\mathbf{r}: \mathbb{R}^2\to\mathbb{R}^3\) som definieras genom att \( \mathbf{r}(u,v)= \) \[ \left(v \cos \left(\frac{u}{2}\right) \cos (u)+2 \cos (u),v \sin (u) \cos \left(\frac{u}{2}\right)+2 \sin (u),v \sin \left(\frac{u}{2}\right)\right), \] där \(0\le u\le 2\pi\) och \(-\frac12 \le v \le \frac12\).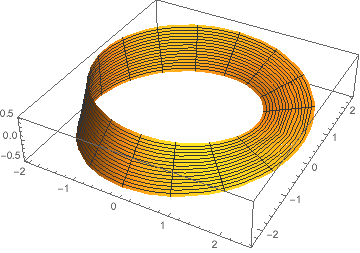
Svar:
En beräkning av normalvektorfältet ger \(\mathbf{n}(u,v)=\)
\[
\left(\sin \left(\frac{u}{2}\right) \left(2 \cos (u)-v \sin \left(\frac{u}{2}\right)
\sin (u)\right),\frac{1}{2} \left(v \left(\sin ^2(u)+\cos (u)\right)+2 \cos
\left(\frac{u}{2}\right)-2 \cos \left(\frac{3 u}{2}\right)\right),-\cos
\left(\frac{u}{2}\right) \left(v \cos \left(\frac{u}{2}\right)+2\right)\right).
\]
Insättning av punkterna \((0,0)\) och \((2\pi,0)\) ger
\[
\mathbf{n}(0,0)=(0,0,-2) \quad \mathrm{och} \quad \mathbf{n}(2\pi,0)=(0,0,2).
\]
Vi kan alltså konstatera att normalvektorfältet pekar i motsatt riktning efter att ha gått runt ett varv.
Maila för handledning.
Hur upplevde du problemet?
Svårighet:
Relevans:
Svårighet:
Relevans: