Efter videon följer ett problem som du kan lösa för att testa att du tillgodogjort dig innehållet.
Problem:
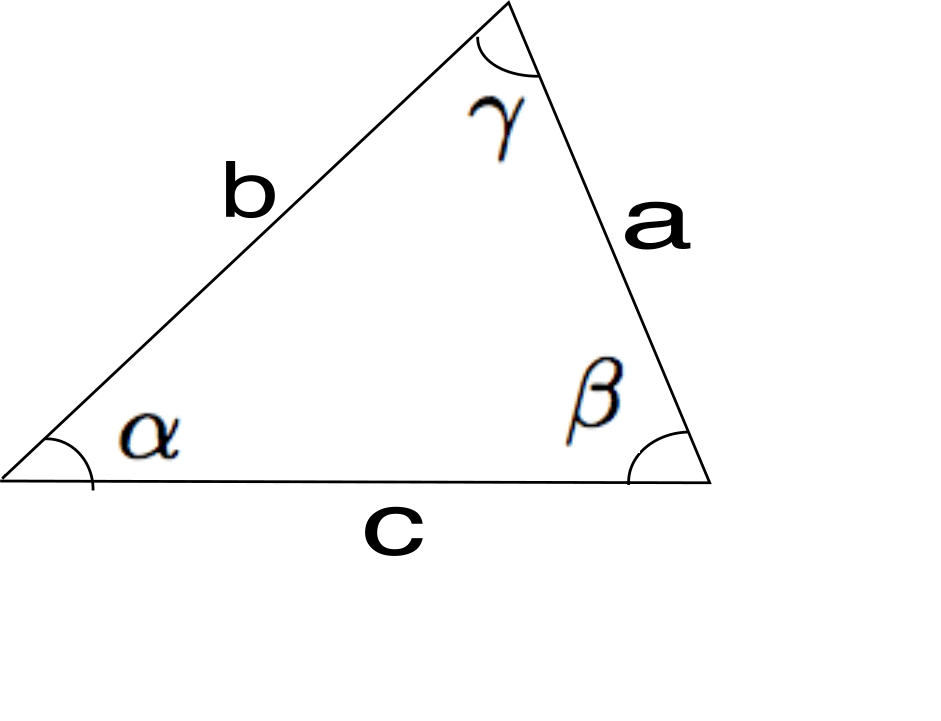
1) Bestäm vinklarna (i radianer) om $a = 4$, $b = 5$ och $c = 6$.
2) Bestäm $b$ och $c$ om $a = 1$, $\beta =\pi/4$, $\gamma = 3\pi/ 8$.
Svar:
a) Cosinus-satsen ger att $a^2=b^2+c^2-2bc\cos\alpha$, vilket ger att \[\cos\alpha =\dfrac{6^2+5^2-4^2}{2\cdot 5\cdot 6}=\frac34 \Rightarrow \alpha\approx 0.72.\]På samma sätt får vi \[\cos\beta =\dfrac{6^2+4^2-5^2}{2\cdot 4\cdot 6}=\dfrac{9}{16} \Rightarrow \beta\approx 0.97,\]\[\cos\gamma =\dfrac{4^2+5^2-6^2}{2\cdot 4\cdot 5}=\dfrac{1}{8} \Rightarrow \gamma\approx 1.45.\]
Svar: $\alpha\approx 0.72$, $\beta\approx 0.97$, $\gamma\approx 1.45$.
b) Vi ser först att $\alpha =\pi -\beta -\gamma=\dfrac{3\pi}{8}$. Enligt sinussatsen är\[\dfrac{\sin\alpha}{a}=\dfrac{\sin\beta}{b}=\dfrac{\sin\gamma}{c},\] dvs.\[\dfrac{0.924}{1}=\dfrac{0.707}{b}=\dfrac{0.924}{c},\]vilket ger $b\approx 0.765$ och $c=1$.
Svar: $\alpha\approx 0.72$, $\beta\approx 0.97$, $\gamma\approx 1.45$.
b) Vi ser först att $\alpha =\pi -\beta -\gamma=\dfrac{3\pi}{8}$. Enligt sinussatsen är\[\dfrac{\sin\alpha}{a}=\dfrac{\sin\beta}{b}=\dfrac{\sin\gamma}{c},\] dvs.\[\dfrac{0.924}{1}=\dfrac{0.707}{b}=\dfrac{0.924}{c},\]vilket ger $b\approx 0.765$ och $c=1$.
Maila för handledning.
Hur upplevde du problemet?
Svårighet:
Relevans:
Svårighet:
Relevans: