Efter videon följer ett problem som du kan lösa för att testa att du tillgodogjort dig innehållet.
Problem:
Beräkna a) $\cos t$, b) $\sin t$, c) $\tan t$ och d) $\cot t$, där $t$ är vinkeln i figuren $\triangle ABC$.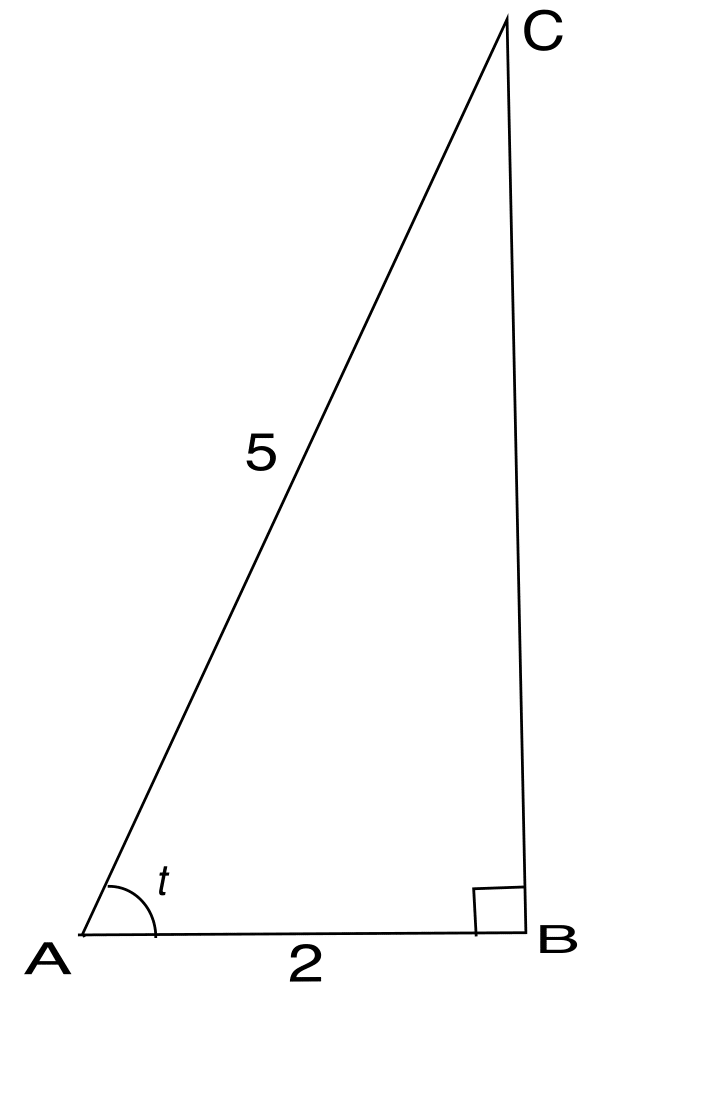
Svar:
Det framgår direkt av figuren att $\cos t=\dfrac25$.
För att bestämma $\sin t$ måste vi först beräkna höjden $h$ ($=|BC|$). Pythagoras sats ger att $h^2+2^2=5^2$, dvs. $h=\sqrt{25-4}=\sqrt{21}$. Alltså blir $\sin t=\dfrac{\sqrt{21}}{5}$.
Vi får vidare $\tan t=\dfrac{\sin t}{\cos t}=\dfrac{\sqrt{21}}{2}$ och $\cot t=\dfrac{1}{\tan t}=\dfrac{2}{\sqrt{21}}$.Sammanfattningsvis gäller $\cos t=\dfrac25$, $\sin t=\dfrac{\sqrt{21}}{5}$, $\tan t=\dfrac{\sqrt{21}}{2}$, $\cot t=\dfrac{2}{\sqrt{21}}$.
För att bestämma $\sin t$ måste vi först beräkna höjden $h$ ($=|BC|$). Pythagoras sats ger att $h^2+2^2=5^2$, dvs. $h=\sqrt{25-4}=\sqrt{21}$. Alltså blir $\sin t=\dfrac{\sqrt{21}}{5}$.
Vi får vidare $\tan t=\dfrac{\sin t}{\cos t}=\dfrac{\sqrt{21}}{2}$ och $\cot t=\dfrac{1}{\tan t}=\dfrac{2}{\sqrt{21}}$.Sammanfattningsvis gäller $\cos t=\dfrac25$, $\sin t=\dfrac{\sqrt{21}}{5}$, $\tan t=\dfrac{\sqrt{21}}{2}$, $\cot t=\dfrac{2}{\sqrt{21}}$.
Maila för handledning.
Hur upplevde du problemet?
Svårighet:
Relevans:
Svårighet:
Relevans: